Можно указать несколько случаев, когда более сложные и, следовательно, более реалистические возрастные структуры удается описать с помощью модели Маккендрика фон Фёрстера и ее обобщения. Мы не будем предпринимать попыток решить соответствующие уравнения, а ограничимся изложением возможностей, присущих формализму.
Прежде всего, напомним наиболее общую форму – модели в случае одного отдельного вида:
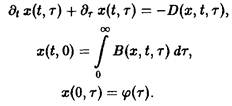
Множество самых различных решений определяется выбором функций D (x, t, т) и В. В дальнейшем мы обсудим лишь несколько принципиальных вариантов. Соображения, развиваемые ниже относительно функции D, могут быть по аналогии перенесены на рождаемость В.
Прежде всего, мы предположим существование явной зависимости от времени. Это позволит учитывать изменения внешних условий. Колебания могли бы моделировать годичные или более длительные изменения, чередования теплых и холодных периодов, а скачкообразные изменения – влияние природных катаклизмов на экосистемы. Существуют и другие разнообразные условия, приводящие как к положительным, так и к отрицательным последствиям, но их вряд ли уместно классифицировать более подробно.
В дальнейшем мы всегда будем предполагать, что система всегда находится в стационарном окружающем поле. Явная зависимость от времени в этом случае не возникает, но изменение величины D в зависимости от плотности х может быть весьма разнообразным. Рассмотрим сначала простейший случай – зависимость от х,
Несколько более реалистическим является учет ограничивающего члена в виде
препятствующем для К > 1) расходимости 
при 
Если число особей очень велико, то смертность сильно возрастает и система стабилизируется на уровне, зависящем от функций 
i. В 
могут быть включены члены более высокого) порядка. Включение кубической нелинейности может привести к возникновению бистабильных ситуаций, в которых число особей 
может устанавливаться на двух, вообще говоря, не зависящих от г устойчивых значениях.
Однако возможные режимы этим отнюдь не исчерпываются. Особенно большой интерес наряду с перечисленными выше вариантами нелокальных зависимостей представляют такие, которые в простейшей форме могут быть записаны следующим образом:
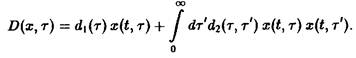
Ядро интеграла 
описывает взаимодействие между особями самых различных возрастов внутри одного вида. При 
эффективная смертность особей, достигших возраста г, понижается за счет наличия особей возраста 
. Примером может служить, например, особенно тщательная забота о потомстве на протяжении первых отрезков жизни или поддержка старых, весьма опытных особей. Соответственно, 
приводит к внутривидовой конкуренции, проявляющейся в борьбе за верховенство или в "конфликтах поколений". Как и в соотношение, в формулу могут входить члены высшего порядка, описывающие взаимодействие между тремя и более различными возрастными группами.
Статьи и публикации:
Система крови
Под системой крови понимают совокупность органов, тканей и некоторых физиологических процессов, которые обеспечивают образование крови и ее функционирование. В эту систему входят:
органы, где происходит образование и разрушение клеток кр ...
Биосоциальная природа человека
В процессе антропогенеза (эволюционно-исторического процесса формирования человека) произошло возникновение на нашей планете высшей формы существования материи – социальной. Появление человека является результатом развития жизни в одной и ...
Микроэмульсии как растворители для органического синтеза
Использование микроэмульсий в органическом синтезе оказалось чрезвычайно полезным, поскольку они способны солюбилизировать полярные и неполярные компоненты, а также пространственно разделять или концентрировать реагенты. Дальнейшее обсужд ...