Модель старения Маккендрика фон Фёрстера

Для математического описания индивидуального развития Маккендрик и фон Фёрстер разработали рекуррентную модель, в которой непрерывный процесс старения рассматривается как последовательность отдельных, изолированных, актов. С математической точки зрения речь идет о том, чтобы вывести систему дифференциальных уравнений для функции плотности x, описывающей, сколько особей возраста г существуют в системе в момент времени t. Рассмотрим такую систему TTTTTTTTTTTTTTTTTTTTTTTTTTTTTTTT

в момент времени t + At. Число особей, которые к этому времени достигнут возраста г, равно числу особей, которые к моменту времени t достигли возраста г – At, за вычетом особей, умерших за интервал времени At. В результате мы получаем:

где D – смертность. Совершая предельный переход при At – О, приходим к дифференциальному уравнению

Важную роль в динамике системы играют также процессы воспроизводства, характеризуемые рождаемостью В. Эта величина показывает, сколько потомков производят в момент времени t особи, достигшие возраста т. В качестве начального условия по г для уравнения мы получаем величину

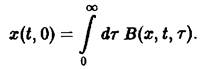
Оно дополняется заданием второго начального условия

Уравнения, с начальными условиями, задают модель Маккендрика–фон Фёрстера для популяций с возрастной структурой. Эта модель позволяет определить временную эволюцию функции плотности x по заданному начальному распределению у, если известны скорость воспроизведения и смертность. Решения, получаемые в рамках этой модели при различных конкретных функциях D и В, подробно изучены (McKendrick, 1926; von Foerster, 1959; Полу-эктов, 1974; Полуэктов и др., 1980; Романовский и др., 1984). Смертность D и рождаемость В, вообще говоря, сложным образом зависят от плотности x и), что приводит к существованию разнообразных структур решений. Однако уравнения в этом случае также становятся весьма сложными, и их аналитическое решение становится невозможным. Поэтому мы сначала рассмотрим простейший случай, когда рождаемость и смертность линейны по плотности x и не зависят явно от времени:

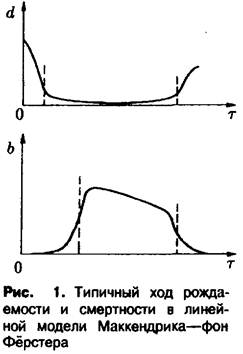
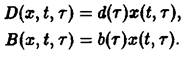
Реалистические примеры функцийи представлены на рис. 1. Смертность по прошествии первого времени после рождения стабилизируется на относительно низком уровне и начинает снова возрастать лишь при больших г; в дальнейшем мы, кроме того, принимаем предположение

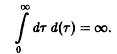
Рождаемость, как правило, достигает своего максимального значения лишь по истечении определенного периода после начала фазы зрелости и в старости снова понижается.

Учитывая соотношения, мы получаем из уравнений – систему уравнений

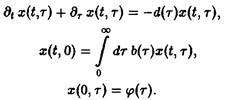
Поведение решений системы уравнений вполне очевидно. Из первого уравнения мы получаем, прежде всего, вероятность W того, что особь достигает возраста т:

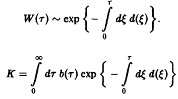
В зависимости от величины К возможны три качественно различных случая. При К > 1 число новорожденных в единицу времени больше числа умерших, доминируют процессы воспроизводства, и при t → оо мы получаем при всех г расходящуюся плотность x – оо. Наоборот, при К<1 воспроизводство слишком слабо, и при t – оо мы получаем x –* О при всех т, т.е. вид вымирает. Наконец, при К = I оба процесса находятся в равновесии, соответственно, существует бесконечно много стационарных состояний, и только от начального условия <р зависит, какое из них реализуется. Разумеется, в случаях К > 1 и К < 1 результат не зависит от начального условия <р.

Тем самым мы получаем качественную характеристику динамики индивидуального развития внутри отдельного вида при упрощающем предположении. Исследуем теперь, какие модификации возникают в том случае, когда п видов развиваются в соответствии с уравнениями, аналогичными уравнению, и, кроме того, взаимодействуют между собой посредством процесса отбора. Затронутая проблема связана с вопросом оптимальной стратегии старения, сложившимся в ходе эволюции.

Статьи и публикации:

Пищеварение в желудке. Функции и строение желудка. Железы желудка. Методы изучения секреторной функции желудка
В желудок поступает значительный объем пищи. Там она находится от 5-6 до 10 часов. Срок пребывания зависит от рода пищи: богатая белками, особенно растительными, пища задерживается в желудке дольше, чем углеводная. Еще более длительно ост ...

Сравнение укоренения черенков сортов ͵Little Princess΄ и ͵Golden Princess΄
Лучше укоренились черенки спиреи японской сорта ΄Golden Princess΄, чем черенки сорта ΄Little Princess΄, так как прирост черенков сорта ΄Golden Princess΄, обработанных стимулятором роста "Корневином" ...

Покровные ткани
Они исполняют роль пограничного барьера, отделяя ниже лежащие ткани от окружающей среды. Первичные покровы растения состоят только из живых клеток. Вторичные и третичные покровы – в основном из мертвых с толстыми клеточными стенками. Осн ...