Прежде всего систему п не взаимодействующих между собой видов можно описать уравнениями, обобщающими уравнение:
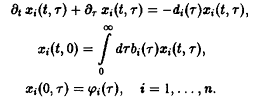
В качестве простого метода создания давления отбора мы по аналогии с моделью Эйгена потребуем постоянства общего числа особей в системе:
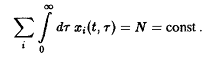
Чтобы условие выполнялось, необходимо модифицировать систему уравнений 13, что можно осуществить различными способами. Особый интерес представляют две возможности.
1. Введение потоковых членов в модель Эйгена.
Такая операция соответствует подстановкам
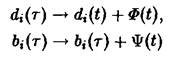
в уравнение, причем во избежание патологии, например, отрицательных концентраций, должны выполняться неравенства
![]()
2. Регуляция скорости воспроизведения.
Регуляция достигается с помощью подстановки
![]()
И в том, и в другом случае существенно, что модификации либо видо-, либо возрастоспециф ич ны.
Если равенство продифференцировать по времени и воспользоваться уравнением с подстановками, то получится следующее:
![]()
где по определению
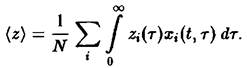
Учитывая положительность
![]()
мы получаем
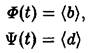
и, наконец, приходим к системе уравнений
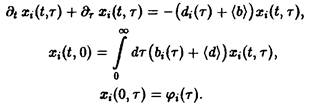
Проводя аналогичные вычисления с использованием подстановок, получаем, полагая
![]()
систему уравнений
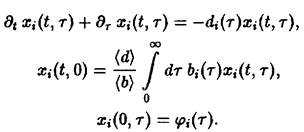
Уравнения и описывают временную эволюцию систем стареющих конкурирующих между собой видов и тем самым удобны для математического анализа индивидуального развития и отбора.
В отличие от системы уравнений для независимых видов дифференциальные уравнения и связаны между собой через определенное соотношением среднее значение. С одной стороны, эта связь выступает как математическое выражение взаимодействия между видами, а с другой – исключает возможность получения аналитических решений и обусловливает тем самым весьма широкое применение численных методов.
Ряд интересных утверждений может быть высказан и без явного решения системы уравнений. В частности, необходимо выяснить, каким образом, зная функции d, и Ь, можно определить те виды, которые замещают другие и поэтому доминируют при больших временах.
Необходимый для этого качественный анализ динамики удается осуществить с помощью подстановок
![]()
где
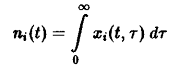
– общее число частиц,
![]()
– нормированная возрастная структура i-ro рода. Рассмотрим сначала ситуацию, описываемую уравнением. Пользуясь подстановкой, получаем следующие уравнения для п, и pi:
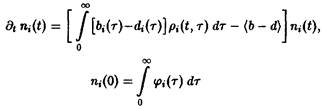
Статьи и публикации:
Замыкающие межклеточные контакты. Рыхлые или простые
контакты
Простой контакт — соединение клеток за счет пальцевидных впячиваний и выпячиваний цитомембран соседних клеток. Специфических структур, формирующих контакт, нет.
Простые контакты занимают наиболее обширные участки соприкасающихся клеток. ...
Антон Романович Жебрак
Антон Романович Жебрак (белор. Антон Раманавіч Жабрак, 14 (27) декабря 1901 дер. Збляны, ныне Гродненской обл. — 20 мая 1965) — советский генетик и селекционер. Академик АН БССР (1940), президент АН БССР с мая по ноябрь 1947 г. Кавалер ор ...
Активаторы и ингибиторы процесса
Для получения глутаминовой кислоты и для интенсивного ее накопления необходим кислород, т.е. необходима аэрация питательной среды. В условиях недостаточной аэрации активируется аланиндегидрогеназа, катализирующая образование аланина из пи ...

