Суммарное давление в i-ом сосуде равно:
Здесь 
- гидростатическое давление, пропорциональное величине действующей перегрузки и отсчитываемое от выбранного нулевого уровня (обычно от уровня нижней точки тела или уровня сердца);
TTTTTTTTTTTTTTTTTTTTTTTTTTTTTTTT
- давление в тканях, окружающих i-ый участок сосудистого русла:
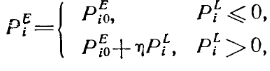
причем 
- избыточное давление на поверхности тела в зоне i-го элемента модели;
- внесосудистое давление в тканях в условиях физиологической нормы
ŋ
- коэффициент передачи давления, ŋ ≤1.
Эти уравнения полностью описывают биомеханическую модель кровообращения в условиях измененной весомости и перепадов давления по телу. Для учета физиологических компенсаторных реакций в модель дополнительно вводится контур автоматического регулирования давлений крови в зонах аорты и каротидных синусов. В качестве регулируемых параметров приняты частота и сила сердечных сокращений, а также сопротивление, податливость и ненапряженный объем участков сосудистого русла. Отклонение давлений в контролируемых зонах от исходных "нормальных" значений (давления в покое в позе "лежа") приводит к включению схемы пропорционального регулирования вышеперечисленных параметров, причем для каждого из них справедливо уравнение
где Δα
- отклонение регулируемого параметра от исходного значения
kα
- коэффициент усиления;
Тα
- постоянная времени для этого параметра.
Пример использования описанной модели кровообращения для исследования реакций организма на воздействие повышенной весомости приведен на рисунке 2:
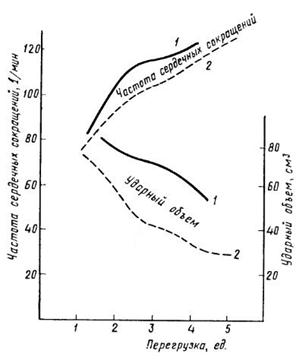
Рис.2. Изменение параметров кровообращения при повышенной весомости. 1 - эксперимент, 2 - расчет.
Видно, что расчетные кривые хорошо отражают качественное изменение физиологических параметров. Практически это означает, что рассмотренный метод расчетной оценки может быть использован для проведения модельных экспериментов по исследованию влияния параметров перегрузки (значение, длительность, скорость нарастания, направление относительно тела человека) и эффективности средств защиты (изменения положения тела, величины, локализации, режима приложения избыточного давления к различным участкам тела). При этом можно ожидать, что полученные результаты будут достаточно надежными, по крайней мере в качественном плане ("лучше","хуже","больше на 30-40%" и т.д.).
Еще более интересной представляется возможность количественного прогнозирования функциональной прочности организма в условиях повышенной весомости, в частности при использовании различных средств компенсации. Для решения этой задачи рассмотренная модель кровообращения нуждается в двух модификациях. Первая, более простая, состоит в уточнении некоторых аналитических соотношений (прежде всего регуляторных) и числовых параметров модели, вторая - в выборе критерия функциональной прочности, учитывающего состояние сознания и уровень работоспособности. Критичным в этом плане является кровоснабжение головного мозга, так что искомый критерий К будет функцией одного или нескольких показателей мозгового кровотока (например, давления крови в тканях мозга, кровенаполнения и/или объемного кровотока).
Пусть в i-ом модельном эксперименте значение величины К (t) упало до уровня Ki* к моменту времени, когда в реальных условиях возникли нарушения сознания и недопустимое снижение работоспособности оператора. Среднее значение K*, полученное при моделировании ряда экспериментальных режимов, даст искомый критерий. Если теперь при модельном анализе нового режима воздействия окажется, что расчетное значение К (t) во всех случаях превышает критическое K*, то можно с некоторой вероятностью считать рассматриваемое воздействие переносимым, а используемые средства компенсации - эффективными.
Статьи и публикации:
Адгезионные или сложные межклеточные контакты
Сложные или адгезионные межклеточные соединения представляют собой небольшие парные специализированные участки плазматических мембран двух соседних клеток. Они подразделяются на запирающие (изолирующие), сцепляющие (заякоривающие) и комму ...
Органы дыхания
К органам дыхания относятся: легкие, где происходит газообмен между воздухом и кровью, и воздухопроводящие пути, по которым проходит воздух в легкие и из них обратно в окружающую среду. Воздух из окружающей среды последовательно проходит ...
Зарождение жизни
Земля сформировалась, вероятно, 4,5–5 млрд. лет назад из гигантского облака космической пыли. частицы которой спрессовались в раскаленный шар. Из него в атмосферу выделялся водяной пар, а из атмосферы на медленно остывавшую Землю в течени ...